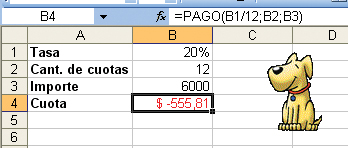
El concepto de Valor Actual pertenece a la matemática financiera y lo vamos a ilustrar con un ejemplo. Supongamos que queremos comprar un televisor que cuesta $6000 en doce cuotas mensuales. Normalmente, el valor de la cuota no sería de $500 (seis mil dividido por doce), porque no es lo mismo pagar seis mil de una sola vez que hacerlo a lo largo de un año. Se entiende que, por “esperarnos” hasta completar el pago, quien nos vende el televisor nos cobrará cierto interés. Digamos que ese interés es del 20% anual. ¿Cuánto será la cuota en esas condiciones? Lo averiguamos con la función PAGO. Esta función tiene tres argumentos:
- El primero es la tasa.
- El segundo es la cantidad de cuotas.
- El tercero es el valor del bien que estamos comprando.
Si el valor de la tasa está en [B1], la cantidad de cuotas está en [B2] y el importe final está en [B3], el valor de la cuota se obtiene con =PAGO(B1/12;B2;B3). La tasa aparece dividida por doce porque los pagos son mensuales, pero la tasa dada en [B1] es anual. Con los datos del ejemplo, obtenemos una cuota de aproximadamente $555. La función devuelve un valor negativo porque representa dinero que tenemos que pagar, mientras que el valor de [B3] es dinero que recibimos (bajo la forma de un televisor, en este caso).
Como los doce pagos mensuales de $555 cubren los $6000 que cuesta el televisor que nos llevamos hoy, decimos que 6000 es el valor actual de esa serie de pagos. En estos problemas hay cuatro variables:
- El importe.
- El valor de la cuota.
- La cantidad de cuotas.
- La tasa de interés.
La función PAGO calcula el valor de la cuota en función de las otras tres variables. Excel tiene otras tres funciones similares para cada una de las demás variables. Supongamos, por ejemplo, que nos ofrecen comprar un televisor de $7000 en quince cuotas mensuales de $500 cuando la tasa anual de mercado es del 20%. Calculemos el valor actual de estos quince pagos con la función VA (de valor actual). Si la tasa está en [B1], la cantidad de cuotas, en [B2], y el valor de la cuota, en [B3], la función es =VA(B1/12;B2;B3). Con los datos del problema obtenemos un valor actual de $6587. Eso significa que, en términos financieros, estamos pagando menos de lo que vale el televisor y el negocio nos conviene.
También existen las funciones NPER, para calcular la cantidad de cuotas, y TASA, para calcular la tasa de interés. Siempre, en función de las otras tres variables en cada caso.